Der angeschlossene Würfel

[Otmar]

@Friedel:
Genau das macht das Rätsel ja so interessant. Man meint es geht nicht und es geht doch.

Mehr ->

Die Kanten und Flächen eines Würfels sind parallel. Man kann einen Würfel also immer durch jeden beliebigen Ring, der um den Würfel geht, parallelverschieben.

Wenn das so wäre, hättest du recht, aber offensichtlich sind nicht alle Kanten und Flächen parallel zueinander, deshalb baut dein Schluß auf einer falschen Voraussetzung auf und ist als Begründung zur Verneinung einer Lösung des Rätsels ungeeignet.

Irgendwie greift in deinem Zitat der Spoiler nicht. Könntest du meinen Tipp wieder unter einem Spoiler verstecken. Danke!

[Musagetes]

Hallo Otmar,

nachdem 40-jährigen jubilium des Zauberwürfels, habe ich meinen auch wiedermal hervorgekramt.

Was soll ich sagen wieder ein schönes Rätsel das für große verwirrung gesorgt hat.

Erst nach Neulings Lösungsversuch hatte ich eine Vorstellung, wie der Würfel an die Stange angeschlossen werden könnte,
auch wenn das m. E. wenig Sinn macht einen „gesicherten Würfen“ nochmals mit einem Schloss zu verschließen.
Aber ein Rätsel sollte zwar Sinn machen, muss es aber nicht.
Wenn ich ehrlich bin, dann ist mir immer noch nicht ganz klar, da es wohl zwei Möglichkeiten gibt, wie der Würfel angeschlossen wird.

Ich vermute mal, nach den angekündigten Gemeinheiten, dass …..

Mehr ->

die Bohrung im Würfel überflüssig und eine Finte ist.

Nach dieser Vermutung probierte ich mit meinem Zauberwürfel, welche Möglichkeiten es noch gibt, mit einem Kreisring den Würfel so zu „umschlingen“,
dass er nicht aus den Schloss genommen werden kann.

Da ich keine Zeinung anfertigen kann, ist es nur schwer zuerklären wie das Schloss um den Würfel gelegt wird, wenn das der gesuchte Weg ist,
kann ja evt. Otmar hier helfen.



Man legt den Schlossring oberhalb von H auf die Deckfläche, geht unterhalb um E und G um den Würfel herum und verschließt in unterhalb von B auf der Würfelunterseite.

Hoffe, das war verständlich genug!

Nun liegt der Schlossring auf sechs Auflagepunkten in der Form des u. a. Sechseckes auf.



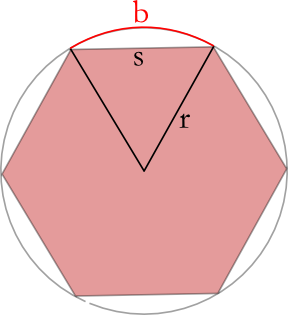
Das Sechseck, kann nun als gedachte Ebene optimal in den Würfel legen.

Jetzt kann man folgende Beziehungen zwischen dem Würfel und dem Sechseck finden.

Wenn h die „Höhe“ (Abstand der parallelen Sechseckseiten) des Sechseckes ist,

dann ist nach dem Pythagoras der gesuchte Innenradius des Kreisringes

r= sqrt(h^2 +s^2)/2

Strecke A-B des Würfels ist a=1 und der Abstand A-X (X soll der untere linke Auflagepunkt des Sechseckes sein) wird mit der Strecke X bezeichnet.

Demnach ist nach dem Pythagoras s^2= 2(a-x)^2

Wenn man im Würfel vom oberen linken Auflagepunkt eine senkrechte Strecke zum Würfelboden projiziert, ist der Abstand von diesem projizierten Punkt
zur Ecke A gleich die Strecke X. Nun lässt sich ebenfalls nach den Pythagoras von dem projizierten Punkt die Strecke y zu den dem Auflagepunkt „X“
berechnen.

y^2= 2x^2

Nun lässt sich wieder nach dem Pythagoras die „Höhe“ h (Abstand der parallelen Sechseckseiten) des Sechseckes berechnen.

h^2 = a^2 +y^2
y ersetzt
h^2 = a^2 +2x^2


Nun dürfte man alle relevanten Größen berechnet haben und kann sie in die Ausgangsgleichung einsetzen.

r= sqrt(h^2 +s^2)/2
r= sqrt(a^2 +2x^2+s^2)/2
r= sqrt(a^2 +2x^2+2(a-x)^2)/2

Nach einer Minimum Extremwertberechnung für r erhält man.

r = 1/sqrt(2)

r = 0,7071m

Demnach ist der Innendurchmesser d = 142cm

Ich hoffe, auch wenn es etwas schwierig war, dass ihr meinen Ausführungen folgen konntet.

So nun dürft Ihr alle wieder mit eurem Zauberwürfel spielen!

Viele Grüße
Musagetes

[Neuling]

Hallo Musagetes!

Mehr ->

Ohne deinen Lösungsweg im Einzelnen nachzuvollziehen - ein Ring mit einem Radius von 0,7071m um einen Würfel von 1m Kantenlänge, lässt diesen Würfel glatt durchrutschen. Dieser Radius ist doch die halbe Würfelflächendiagonale ?

Und wo befindet sich in deiner Lösung eigentlich die Stange ?

LG Neuling

[Otmar]

Dann mal herzlichen Glückwunsch an Musagetes! und
Die Lösung ist richtig! Das entscheidende neben der Längenangabe ist die Erklärung, wie der Ring um den Würfel liegt. Ich hebe das nochmal hervor:

Mehr ->

Man legt den Schlossring oberhalb von H auf die Deckfläche, geht unterhalb um E und G um den Würfel herum und verschließt in unterhalb von B auf der Würfelunterseite.

Natürlich braucht man dazu die Skizze von Musagetes.

@Neuling:

Mehr ->

So verblüffend es ist, der Ring hat genau den gleichen Durchmesser, wie eine Diagonale einer Seitenfläche des Würfels. Das stimmt. Aber er liegt nicht so, dass man ihn abstreifen kann, sondern "verhakt sich" zwischen sechs Ecken des Würfels.

Ich fang mal an, eine Zeichnung zu meiner Lösung zu machen.

Das Originalrätsel, ohne Bohrung, stammt übrigens von Heinrich Hemme. Praxis der Mathematik in der Schule, Ausgabe 45, 2003 Seite 173 und 174.

[Otmar]

Nun will ich langsam mal mit der Lösung beginnen. Erst mal eine Skizze:

Mehr ->

wuerfel1.png (8.21 KiB) 1250-mal betrachtet

Oben links sieht man den Würfel so auf eine Ecke gestellt, dass eine der Raumdiagonalen senkrecht auf dem Fußboden steht. Rechts daneben sind zwei Ebenen angedeutet, die oben und unten vom Würfel eine dreiseitige Pyramide abschneiden. Dabei entstehen zwei Schnittflächen, die beide gleichseitige Dreiecke sind mit der Kantenlänge einer Flächendiagonale des Würfels. Auf die untere Schnittfläche wird der verbliebene Würfelrest hingelegt. Im Bild links unten sieht man das genau von oben. Die obere Schnittfläche ist rot eingefärbt. Rechts daneben sind nur noch Schnittflächen (oben in rot und unten in grün) und Kanten des Würfels gezeichnet. Weiterhin liegt in einer horizontalen Ebene auf halber Höhe des Würfelrestes das Ringschloss um die sechs verbliebenen Kanten des Würfels. Der Durchmesser muss größer oder gleich einer Flächendiagonale des Würfels sein, da die gegenüberliegenden Kanten ja parallele Kanten des Würfels im Abstand der Flächendiagonale sind. Also mindestens Wurzel aus (100²+100²)cm². Das Schloss hat also 142 cm Durchmesser.

Das Abschneiden der Ebenen ist natürlich zum Befestigen des Würfels mit dem Schloss nicht nötig, sondern diente nur für eine vielleicht bessere räumliche Vorstellung und einfachere Zeichnung.

Jetzt zur Stange: Man kann nun eine der 6 Ebenen, über die das Schoss gelegt ist, auswählen und noch eine dünne Stange durchstecken, oder andres herum den Würfel an der dünnen Stange im Zimmer anschließen, dass er nicht gestohlen werden kann. Damit wäre die Aufgabe zum Teil gelöst. Zeigen muss ich noch, dass keines der genannten Schlösser durch die Bohrung passt, dass man das Ringschloss nicht vom Würfel lösen kann und dass es kein kleineres Ringschloss gibt, welches auch zum Anschließen des Würfels geeignet wäre.

[Otmar]

Für Schloss und Bohrung erhält man mit folgender Skizze,

Mehr ->

die eine Schnittdarstellung von Schloss und Würfel sein soll.

wuerfel2.png (4.27 KiB) 1242-mal betrachtet

Der Kreisring mit innerem Radius r soll gerade so in die Bohrung mit Durchmesser d passen. Man erhält eine Gleichung:
d = h + r/20, denn der Kreisring ist ja so breit wie 5% von r. Eine zweite Gleichung ist:
r²=50²+(r-h)², wenn alle Längen in cm angegeben sind. Hier ist h der maximale Abstand des inneren Kreises von der senkrecht darunter liegenden Mantelfläche der Bohrung. Wenn man die erste Gleichung nach h umstellt und in die zweite einsetzt, bekommt man eine quadratische Gleichung in r mit den Lösungen:
r=(420 d - 200 Wurzel(4d²-1025))/41 und
r=(420 d + 200 Wurzel(4d²-1025))/41
Weil in Zentimetern d=16 ist, steht unter der Wurzel 4*16²-1025=-1. Die Wurzel ist also keine reelle Zahl, was nichts anderes bedeutet, als dass es keinen passenden Radius für ein Ringschloss gibt. Also schon gar kein Ringschloss zum Anschließen möglich ist, bei dem der Innendurchmesser in cm ganzzahlig sein soll. Die Bohrung hilft also nicht weiter, den Würfel zu sichern.

Tatsächlich ist es knapp. Schon bei d=16,01cm wird der Term unter der Wurzel positiv und die beiden Lösungen geben uns den kleinsten und größten Radius an. Nehmen wir den Radius mal Zwei erhalten wir zwei Werte für den kleinsten und größten Durchmesser, der dann von 323 bis 333 cm betragen darf. (Das hat Neuling schon ausgerechnet.)
Soll die Bohrung allerdings tatsächlich zur Lösung beitragen, müsste ihr Durchmesser in Millimeterauflösung wenigstens 24,2cm groß sein, so dass Ringschlösser mit Innendurchmessern kleiner oder gleich 142cm durchpassen.

Wer mit dem Rätsel seine Freunde nicht nur aufs Glatteis führen möchte, sondern auch eine Sturz in Kauf nimmt, könnte als Durchmesser der Bohrung 24cm angeben.

[Otmar]

Nun eine Begründung, warum das Schloss sich nicht abstreifen lässt:

Mehr ->

Angenommen, das Schloss lässt sich vom Würfel absteifen. Die Ebene in der sich das Schloss befindet, wird im angeschlossenen Zustand von genau 6 Kanten des Würfels durchstoßen. Nach dem Abstreifen liegt aber keine Kanten des Würfels noch in der Schlossebene. Betrachten wir den Zeitpunkt, zu dem erstmals eine der genannten sechs Kanten die Schlossebene verlässt. In dem Moment befindet sich eine Ecke des Würfels in der Schlosseben. Diese Ecke habe ich mit dem Buchstaben C bezeichnet und in den drei Abbildungen unten markiert.

wuerfel3.png (7.56 KiB) 1215-mal betrachtet

Im mittleren Bild sieht man die Schlossebene innen hellblau eingefärbt und in schwarz die Schnittlinien des Würfels mit der Schlossebene. Die Kanten, die die Würfelecke, die C gegenüber liegt, gemeinsam haben, schneiden die Schlossebene in den Punkten A und B und ragen mit den Längen x cm und y cm auf einer Seite der Ebene heraus. Dabei ist sowohl 0<=x<=100 als auch 0<=y<=100. x und y sind sogar noch kleiner. Denn a und b (Längen in cm) sind höchstens 142 (Innendurchmesser d des Ringschlosses in cm). In der rechten Grafik findet man zwei rechtwinklige Dreiecke mit gelben Katheten für die gilt: a²=2*100²+y² und b²=2*100²+x² also y²=a²-2*100²<=142²-2*100²=164. Also ist wegen 13²=169 ist sowohl y als auch x kleiner als 13. Nun ist c²=(100-x)²+(100-y)²>=(100-13)²+(100-13)²=15138 und damit kann man erst mal feststellen, dass c>123 sein muss. Aber dass kann nicht sein. Denn c muss relativ klein sein.

wuerfel4.png (5.92 KiB) 1215-mal betrachtet

c wäre am größten, wenn die Punkte A, B und C direkt am Schloss anliegen würden und a und b so klein wie möglich wären. a und b sind aber nach obigen Gleichungen mindestens so groß wie eine Flächendiagonale s (Länge in cm) des Würfels. In den rechtwinkligen Dreiecken mit den Kanten d, z, und s im rechten Bild ist z²=d²-s²=164. Also z<13. Damit ist c<26 und der gewünschte Widerspruch zu c>123 bestätigt, dass sich das Schloss nicht abstreifen lässt.

[Otmar]

Und zum Schluss noch eine Begründung, warum das ausgewählte Ringschloss das kleinste ist.

Mehr ->

Nimmt man an, man könnte den Würfel mit einem Schloss mit Innendurchmesser d <= 141cm anschließen, dann kann die vom Schloss umschlossene Kreisfläche K mit Durchmesser d nicht von zwei parallelen, diagonal gegenüberliegenden Würfelkanten durchbohrt werden, denn der Abstand dieser Kanten ist etwas größer als 141cm.

würfel5.png (7.85 KiB) 1213-mal betrachtet

Erster Fall: Zwei gegenüberliegende Kanten einer Außenfläche gehen durch K. Man kann diese Außenfläche nach oben legen, so wie ganz links oben im Bild gezeichnet. Die genannten beiden Kanten sind grün und der Schnitt der Schlossebene mit der Außenfläche ist blau gezeichnet. Sollte nun die Grundfläche des Würfels nicht in K liegen, dann kann man das Schloss nach oben abziehen. Also gehen auch Kanten der Grundfläche durch K. Allerdings darf das Schloss nicht durch die roten Kanten im Bild oben rechts gehen, da jede rote Kante eine diagonal gegenüberliegende grüne Kante hat, die bereits in K liegt. Es müssten also beide gelbe Kanten durch K gehen. Das geht aber nicht, weil der Schnitt der Schlossebene in Grund und Deckfläche dann nicht parallel wäre, was aber offenbar so sein muss, denn werden zwei parallele Ebenen durch eine dritte geschnitten, dann sind die beiden Schnittgeraden parallel. Also tritt der erste Fall nicht ein.

Zweiter Fall: Es gibt keine Außenfläche, bei der zwei gegenüberliegende Kanten durch K gehen. Dann muss wenigstens eine Außenfläche über Eck von K geschnitten werden. Man kann diese Außenfläche wieder nach oben legen, wie in der Grafik links unten. Geht nun von einer grünen Kante der Schnitt weiter zu der gelben Kante, dann muss auch von der anderen grünen Kante der Schnitt zum gleichen Punkt der gelben Kante gehen, so wie unten in der Mitte gezeigt. Das Schloss lässt sich dann natürlich abziehen. Also muss der Schnitt in den Seitenflächen zu beiden roten Kanten weitergehen, denn es kann nur über Eck geschnitten werden. Aber dafür ist das Schloss zu klein, denn die beiden roten Kanten liegen ja diagonal gegenüber.

Dritter Fall. K schneidet gar keine Außenfläche. Damit auch keine Würfelkante. Offenbar ist in diesem trivialen Fall der Würfel nicht gesichert.